2022年河南省考行測備考 方程問題未知數的設法

方程是指含有未知數的等式。在數量關系中，解方程容易，但如何設未知數，正確的列出等量關系是一個難點，下面我們結合具體的題目分別講解。

1.設所求量

例：(2020重慶)某企業員工組織周末自駕游，集合后發現。如果每輛小車坐5人，則空出4個座位;如果每輛小車少坐1人，則有8人沒坐上車，那么，參加自駕游的小車有：

A.9輛 B.10輛 C.11輛 D.12輛

解析：拿到一個題目，我們優先選擇設所求量，簡單粗暴，求誰設誰，可以直接設有X輛小車，通過兩種安排員工的坐車方式的總人數相等，找出等量關系，在本題中出現的“如果…如果…”是一種天然的等量關系;

第一種坐車方式求員工人數：5X-4;第二種坐車方式求員工人數：4X+8;

5X-4=4X+8，解得X=12，選擇D項;

本題小結：簡單直接，優先設所求量。

2.設比例份數

例：(2018廣西)年終某大型企業的甲、乙、丙三個部門評選優秀員工，已知甲、乙部門優秀員工數分別占三個部門總優秀員工數的1/3和2/5，且甲部門優秀員工數比丙部門的多12人，問三個部門共評選出優秀員工多少人?

A.120人 B.150人 C.160人 D.180人

解析：在本題中，直接設優秀員工的總人數進行列式，不方便計算，因此我們考慮在設未知數時，通過題干中的信息，巧妙設置未知數，通過審題“甲、乙部門優秀員工數分別占三個部門總優秀員工數的1/3和2/5”我們可以得知，優秀員工的總人數應是3的倍數以及5的倍數，因此考慮設優秀員工人數為3和5的最小公倍數即15X人，則甲部門優秀員工數為15X×1/3=5X人，乙部門優秀員工數為15X×2/5=6X人，則丙部門優秀員工數=優秀員工的總人數-甲部門優秀員工數-乙部門優秀員工數=15X-5X-6X=4X人;再根據已知條件甲部門優秀員工數比丙部門的多12人找到等量關系，列出方程5X-4X=12，解得X=12人;則三個部門共評選出優秀員工人數為15×12=180人。

本題小結：題干中出現明顯的比例關系時，考慮設比例份數。

3.設中間量

例：(2019江蘇)某機關事務處集中采購了一批打印紙，分發給各職能部門。如果按每個部門9包分發，則多6包;如果按每個部門11包分發，則有1個部門只能分到1包。這批打印紙的數量是：

A.87包 B.78包 C.69包 D.67包

解析：審題后發現，直接設打印紙的數量，不方便計算，但觀察可知，打印紙的數量和部門的數量有關，因此考慮設出部門的數量，即可表示出打印紙的數量，設部門數量為X，按照之前總結的天然等量關系“如果…如果…”，按照第一種分發方式表示出打印紙的數量：9X+6;按照第二種分發方式表示出打印紙的數量：11X-10;列出方程：9X+6=11X-10，解得X=8，故打印紙的數量為9×8+6=78包，選擇B項。

本題小結：當題干中的某個中間量與其他未知量存在聯系時，設中間量可以方便列式。

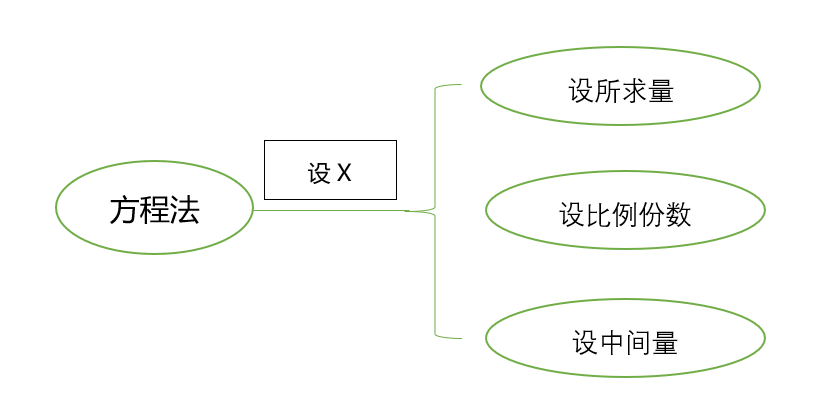
思路總結：

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：