國考行測備考之行程問題中環形跑道模型

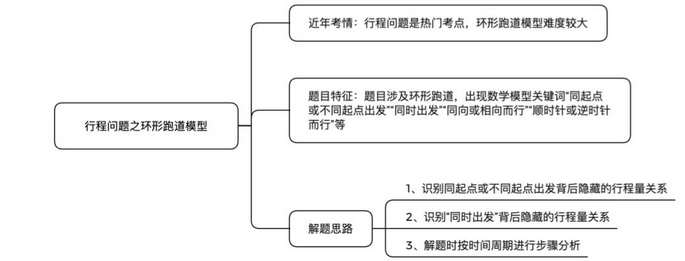
行程問題作為公務員行測考試中的熱門考點，出題范圍較廣，其中比較常見的一類題目是相遇和追及問題，在這類題型中環形跑道模型難度偏大，很多考生由于對這類模型在思維上不熟悉導致無從下手，成為數量關系備考的一大瓶頸。那么對于環形跑道這類模型，到底應該從哪方面入手來進行突破呢?接下來我給大家進行詳細分析。

題目特征：題目涉及環形跑道，出現數學模型關鍵詞“同起點或不同起點出發”“同時出發”“同向或相向而行”“順時針或逆時針而行”等

解題思路：

1、識別同起點或不同起點出發背后隱藏的行程量關系

①同起點出發，反方向(相向)行走，屬于相遇問題，第一次相遇時所走的路程和=環形一圈的長度。

②不同起點出發，反方向(相向)行走，屬于相遇問題，第一次相遇時所走的路程和=環形一圈的長度-初始距離。

③同起點出發，同方向行走，屬于追及問題，第一次追上時的路程差=環形一圈的長度。

④不同起點出發，同方向行走，屬于追及問題，第一次追上時的路程差=初始距離。

2、識別“同時出發”背后隱藏的行程量關系

在時間一定的情況下，路程與速度成正比。

例題講解

【例1】一條環形跑道長400m，小張與小王同時從同一點出發，相向而行，小張的速度為6米每秒，小王的速度為4米每秒，當小王第一次跑回到出發點時，兩人相遇了幾次? A.1

B.2

C.3

D.4

【答案】B

【解析】

題目關鍵信息“同一點出發，相向而行”屬于相遇問題。

第一步：小王第一次跑回原點，所跑路程為400米;

第二步：

第三步：相遇一次這個時間周期內兩人路程和為400米，小王第一次跑回原點時兩人路程和為(400+600)=1000米，1000÷400=2----200米，所以兩人相遇2次。

【例2】一條圓形跑道長500米，甲、乙兩人從不同起點同時出發，均沿順時針方向勻速跑步。已知甲跑了600米后第一次追上乙，此后甲加速20%繼續前進，又跑了1200米后第二次追上乙。問甲出發后多少米第一次到達乙的出發點?

A.180 B.150 C.120 D.100

【答案】A

【解析】

題目關鍵信息“不同起點同時出發”，兩次追上乙，則需要按時間周期進行分析

第一步：

第一個時間周期：從出發到第一次追上乙，初始距離=甲路程-乙路程，題目只給了甲路程這個信息，第一個時間周期沒有辦法推理出其他行程量;

第二步：

第二個時間周期：從第一次追上乙到第二次追上乙，屬于同起點同時出發追及問題，等量關系為，所以

第三步：

賦值甲速度為12，乙速度為7，根據題干信息，第二個時間周期甲速度提速20%，則第一個時間周期甲速度為12÷(1+20%)=10

第四步：

第一個時間周期甲路程：乙路程=甲速度：乙速度，則600：乙路程=10：7，求得乙路程為420米，則初始距離為600-420=180米，所以甲出發180米后第一次到達乙的出發點。

從以上兩道例題我們可以看出，環形跑道模型，要從起點和出發時間點兩個方面考慮問題，解題時按時間周期進行步驟分析，求解行程量。任何復雜的問題都是由幾個簡單的問題組成的，關鍵是如何化繁為簡，才是科學的解決問題的方式。同時注意行程問題同時出發這種時間周期“在時間一定的情況下，路程與速度成正比”這個等量關系的運用。希望對大家在今后行程問題的學習中有解決問題的幫助。

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：