2022省考行測行程問題中的等距離平均速度

行程問題幾乎是每次行政職業能力測試數量關系模塊的必考題型，也是眾多考生復習時覺得比較有難度的一類問題。今天我給大家介紹一下基本行程問題中的等距離平均速度題型。

所謂等距離平均速度，通常指一個物體分別以兩個不同大小的速度，通過一段相等的路程的平均速度。他的基礎運動模型如下：

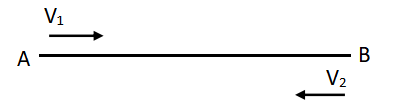
需要注意的是，這里所說的等距離是指以速度V1走過的路程與以速度V2走過的路程相等。在具體應用這個公式時一定要判別清楚題目是否出現這種路程相等的情形。

具體的考題中，簡單的題目運動模式會與上面的基本模型比較相近，比如：

【例1】某人開車從A鎮前往B鎮，在前一半路程中，以每小時60公里的速度前進;而在后一半的路程中，以每小時120公里的速度前進。則此人從A鎮到達B鎮的平均速度是每小時多少公里?

A.60B.80

C.90D.100

在本題中，前一半路程速度為每小時60公里，后一半路程速度為每小時120公里。如下圖，前一半路程長度與后一半路程長度相等，即AC=CB。

近年來的一些新題目，在考查等距離平均速度公式時，設計的運動軌跡與基礎模型還是有一些差異的，這類題目的難度要比【例1】這樣的基礎題目大一些，比如：

【例2】小明每天從家中出發騎自行車經過一段平路，再經過一道斜坡后到達學校上課。某天早上，小明從家中騎車出發，一到校門口就發現忘帶課本，馬上返回，從離家到趕回家中共用了1個小時，假設小明當天平路騎行速度為9千米/小時，上坡速度為6千米/小時，下坡速度為18千米/小時，那么小明的家距離學校多遠?

A.3.5千米B.4.5千米

C.5.5千米D.6.5千米

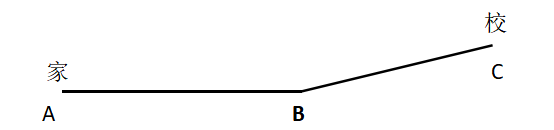
本題中，小明家到學校的路線如上圖所示，根據題意，題目中出現了三個速度數據，能夠滿足應用等距離平均速度公式的是坡路部分，即BC段，而不是從A到C與從C到A。所以，求解時，我們可以先計算BC段的平均速度，再結合AB段的速度確定從家到學校的距離。

相信，通過將以上兩個題目與基本運動模型進行對比講解后，大家能夠對等距離平均速度公式的使用方法理解的更深入。

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：