2022行測省考數量關系倍數特性使用全解

大多數考生在做題時都發現時間不夠用，特別是做數量關系的題目非常耗時間，于是很多同學就戰略性的選擇放棄數量關系。不可否認的是數量關系個別的難題是可以考慮放棄的，但是一些常見的簡單題，各位同學是否要考慮下是不是因為自己的“打開方式”不對，才導致的時間不夠。今天華圖教育為大家整理了行測數量關系——倍數特性使用全解，希望能對各位考生有所幫助。

首先當題目告訴我們諸如一個班級男女生人數之比為7：3或是男生人數占了女生人數的30%，也可以說是，出現比例、百分數、分數基本都是在交代某兩個量之間的倍數特性。這個時候我們就可以迅速操作起來了，如：已知A：B為7:3，此時馬上看問題有沒有問到A、B、A+B、A-B。如果問到了，A是7的倍數，B是3的倍數，A+B是10的倍數，A-B是4的倍數，選項不符合以上倍數特性的都可以排除。而百分數，分數，小數都可以轉化成兩者之比，相當于告訴了兩者的比例關系，所以以后做題多留意誰是誰的幾倍，幾分之幾，百分之幾這樣的信息。接下來請看下面例題：

例題導入

【例1】甲乙丙丁四人一起去踏青，甲帶的錢是另外三個人總和的一半，乙帶的錢是另外三個人的三分之一，丙帶的錢是另外三個人的四分之一，丁帶了91元，他們一共帶了____元。

A.364

B.380

C.420

D.495

【答案】C

【解析】第一步，題目中大量出現誰是誰的幾分之幾，那么前面幾句話相當于交代了甲與另外三人，乙與另外三人，丙與另外三人的比例關系。

第二步，直接看問題，問題問四個人的總錢數，接下來思考這和前面交代的甲的錢是另外三個人總和的一半有什么關系?這句話解讀出來就是告訴你甲：另外三個人=1:2，問題問的所有人的錢，相當于問的是A+B是多少，它對應的是1份+2份得到3份，3的倍數。以此類推，乙是另外三個人的三分之一，總數就是4的倍數，丙是另外三個人的四分之一，總數是5的倍數。綜上，總數既要是3的倍數，又要是4的倍數，還得滿足5的倍數，意思就是必為3、4、5的最小公倍數的倍數。3、4、5最小公倍數為60，則選項必須是60的倍數，只有C選項滿足。

因此，選擇C選項。

【例2】某新型建材生產車間計劃生產480個建材，當生產任務完成一半時，暫時停止生產，對器械進行維修清理，用時20分鐘�；謴蜕�產后工作效率提高了三分之一，結果完成任務時間比原計劃提前了40分鐘，問對器械進行維修清理后每小時生產多少個建材?

A.80

B.87

C.94

D.102

【答案】A

【解析】第一步，題目中提到恢復生產后效率提高了三分之一，則之前的效率：恢復生產后的效率=3:4。

第二步，直接看問題，問題問恢復生產后的效率，選項為4的倍數，只有A選項滿足。

因此，選擇A選項。

以上兩道題是最基本的倍數特性解題，當然出題人也會增加難度，不直接問題題目中提到和比例直接相關的量。比如總的有1300個零件，有三個箱子分別裝滿了零件，大箱子裝的零件數是中箱子的兩倍，問小箱子裝的零件數是多少?

大箱子：中箱子=2:1，問題既沒有問到大箱子中箱子，也沒問到它們之和或者之差。但是，梳理題目信息你會發現大箱子+中箱子+小箱子=總的零件數�？偭慵�數已經告知1300，求小箱子，另外只剩下兩個量了，而此時題目告訴你這兩個量的比例，因此你可以得到大箱子+中箱子總共是3的倍數。所以可以得到一個3的倍數+小箱子=1300。就可以反推1300-選項必須是3的倍數。

【總結】A+B+C+D+…….=總，問題求其中一個量，只需要只要一個具體數據，以及除了這個數據和問題所求量之外的其他量的總份數，就可以用倍數特性去推出答案。

【例3】某足球比賽售出40元、80元、120元門票共2000張，其中80元的門票數是120元的門票數的2倍，比賽門票收入共12萬元。則40元門票售出多少張?

A.1000

B.1150

C.1200

D.1250

【答案】D

【解析】第一步，問題問40元門票。題目中提到80元門票是120元門票的2倍，總門票數為2000張。已知一個具體數據2000，和除了這個總數和問題所求的40元門票之外的80元門票和120元門票的比例關系，即可得到80元與120元門票為3的倍數。

第二步，2000-選項為3的倍數，代入選項發現只有D選項滿足此特征。

因此選擇D選項。

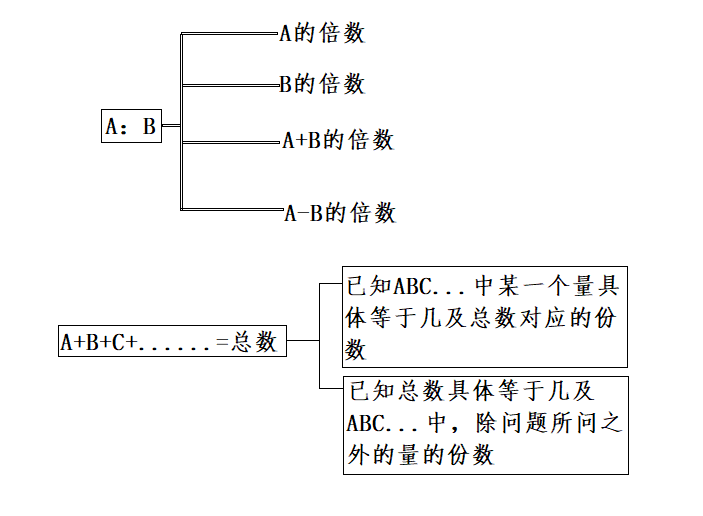
以下是思維導圖，供大家參考：(這件事有趣了…)

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：