數量中一元二次方程和均值不等式的應用

2021年山西省考數量關系題目由往年的10道題增加到了15道題目，題量的增加也顯示出了在公考過程中對數學思維考查的重視程度，結合近年來進面分值要求越來越高，如果考試時完全放棄數量關系題目，就很難拿到一個高分數，也就無法為成功上岸打下良好的基礎。而數量關系之所以難，原因之一是因其題目綜合性強，對考生邏輯思維能力要求較高，但是數量雖難，很多題目卻有著比較強的技巧性，而且一些知識點也在歷年的考試題目當中多次出現，所以如果我們可以學習并掌握這些題目，就能在短時間內求解出這類題目。其中，最值問題便是省考中與其他類型考點結合考查頻率較高的一類，例如幾何求最值，經濟利潤問題求最值，都用到了相應的最值理論，接下來小編就對最值問題進行論述，希望對各位同學有所幫助。

理論知識

1.一元二次方程求最值的應用：，(1)當a>0時，y在處取得最小值;(2)當a<0時，y在處取得最大值。

2.均值不等式理論的應用：a+b≥2(a、b均為正整數，當且僅當a=b時等號成立)。

依據均值不等式，可得對于一個矩形而言，(1)周長C一定時，面積S取得最大值，;(2)面積S一定時，周長C取得最小值，。

解題思路與技巧

觀察題目設問方式，求最大或最小且涉及上述理論知識當中的哪一個，確定后套用公式即可。

例題精講

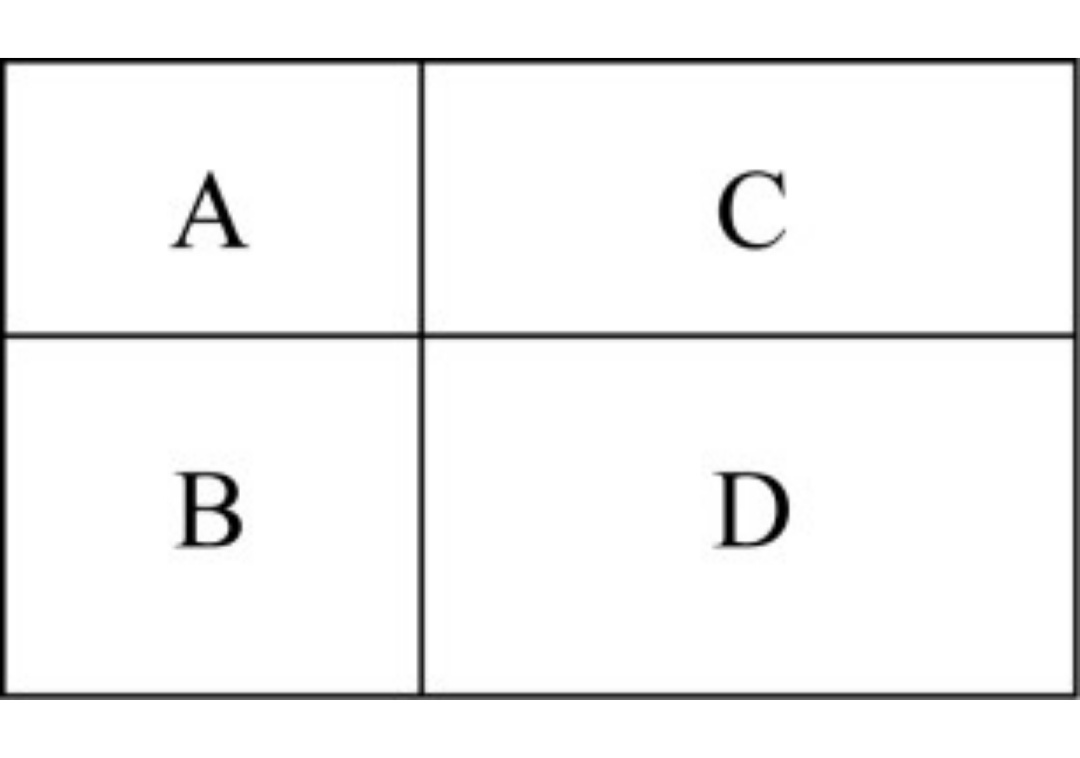
【例1】(2020年聯考)村民陶某承包一塊長方形種植地，他將地分割成如圖所示的4個小長方形，在A、B、C、D四塊長方形土地上分別種植西瓜、花生、地瓜、水稻。其中長方形A、B、C的周長分別是20米、24米、28米，那么長方形D的最大面積是：

A.42平方米B.49平方米

C.64平方米D.81平方米

【答案】C

【解析】第一步，本題考查幾何最值問題。

第二步，設A的長寬分別為a、b，則a+b=10，B與A長相同，設其寬為c，則a+c=12，C與A寬相同，設其長為d，則b+d=14，D與B寬相同，與C長相同，則c+d=(a+c)+(b+d)-(a+b)=12+14-10=16，則D周長為32。

第三步，由均值不等式可得，當周長一定時，面積取得最大值。

因此，選擇C選項。

【例2】(2019年深圳)某類商品按質量分為8個檔次，最低檔次商品每件可獲利8元，每提高一個檔次，則每件商品的利潤增加2元。最低檔次商品每天可產出60件，每提高一個檔次，則日產量減少5件。若只生產其中某一檔次的商品，則每天能獲得的最大利潤是()元。

A.620B.630

C.640D.650

【答案】C

【解析】第一步，經濟利潤問題最值優化類。

第二步，設提升了n個檔次，總利潤為y，根據總利潤=每件商品的利潤×銷售量，可得，令y=0，解得n1=-4，n2=12，當時，y取得最大值。

第三步，y最大值=(8+2×4)×(60-5×4)=640元。

因此，選擇C選項。

根據例題2可以看出通常情況如果將y值寫成兩個數相乘的形式，這樣不需要再記住對稱軸公式，相對更容易求解，節省時間。

綜上可以看出，經濟利潤問題最值優化類以及幾何問題求最值常常是與函數問題相結合，因此，只要大家掌握了函數求最值的相應技巧，這類問題便可迎刃而解!

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：