2022省考行測數量關系“奇偶特性”的樂趣

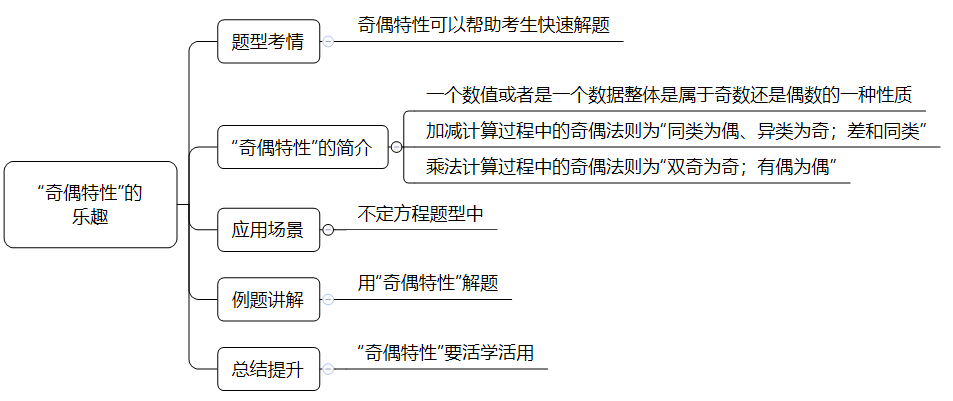
唯快不破，這是行測考試的真理，尤其對于數量關系和資料分析來說，“快”成了制勝的重要法寶。說到“快”，那就不得不提“奇偶特性”了，那么“奇偶特性”到底是一種怎么樣的性質呢?接下來，咱們就詳細地給各位考生介紹何為“奇偶特性”。

1.“奇偶特性”的簡介

所謂的“奇偶特性”，實際上就是指一個數值或者是一個數據整體是屬于奇數還是偶數的一種性質。在解題過程中，奇偶特性能夠幫助考生快速地排除錯誤的選項，從而縮小選擇的范圍。

四則運算中不同的運算，其奇偶法則是不一樣，一般可以歸為兩大類，一類為加減計算過程中的奇偶法則，一類為乘除計算過程中的奇偶法則。

加減計算過程中的奇偶法則為“同類為偶、異類為奇;差和同類”，具體如下：

奇數±奇數=偶數，偶數±偶數=偶數。

奇數±偶數=奇數，偶數±奇數=奇數。

觀察可以發現，在A±B=C的計算過程中，若A、B的都是奇數或者都是偶數時，即A、B類別屬性相同時，他們的計算結果均是偶數，簡稱為“同類為偶”;若A、B類別屬性不同時，即A、B中一個為奇數一個為偶數時，他們的計算結果均是奇數，簡稱為“異類為奇”。

此外，在A±B=C的計算過程中，若A+B的計算結果為奇數，則A-B的計算結果也必然為奇數;若A+B的計算結果為偶數，則A-B的計算結果也必然為偶數;反之亦然。A+B的計算結果代表和，A-B的計算結果代表差，則兩數之和的類別屬性和這兩數之差的類別屬性相同，反之亦然，簡稱為“差和同類”。

乘除計算過程中的奇偶法則，以乘法為主，除法應轉化為乘法后再進行奇偶分析。在乘法計算過程中，其奇偶法則為“雙奇為奇;有偶為偶”，具體如下：

奇數×奇數=奇數;奇數×偶數=偶數;偶數×偶數=偶數。

觀察可以發現，在A×B=C的計算過程中，若A、B的都是奇數時，他們的計算結果是奇數，簡稱為“雙奇為奇”;若A、B中有偶數時，他們的計算結果是偶數，簡稱為“有偶為偶”。

不管是加減計算過程中的奇偶法則，還是乘除計算過程中的奇偶法則，它們都屬于“奇偶特性”，各位考生在做題過程中一定要仔細區分該計算是屬于加減，還是乘除，從而根據不用的運算采用對應的奇偶法則。

2.“奇偶特性”的應用場景

“奇偶特性”通常是應用在不定方程的題型中，因為不定方程正面求解是比較困難的，一般都采用側面分析的方法來確定答案，而“奇偶特性”就是用的比較多的一種側面分析方法了。

如在的運算中，將、、看成三個數據整體，則這三個數據整體在做加法運算，若知道了、、這三個整體中任意兩個數據整體的奇偶屬性，那么就必然能夠根據加減計算的奇偶法則來推出第三個數據整體的奇偶屬性;另外，對于和這兩個整體中，A和x、B和y在做乘法運算，則可根據乘法計算的奇偶法則來判定、這兩個數據整體的奇偶特性。

3.例題講解

【例1】方程的解為，均為質數，則的值為()：

A.194B.197

C.199D.201

【答案】A

【解析】將代入方程，得。因為p、q在做加法，且其計算結果99為奇數，則根據加減計算過程中的奇偶法則中“異類為奇”，可知p、q必然為異類，即一個為奇數一個為偶數。題目求的值，在做乘法計算，且p、q一奇一偶，則有偶數，根據乘法計算過程中的奇偶法則中“有偶為偶”，則的值必為偶數。觀察選項，可以排除BCD，故選A選項。

通過上面的例子，我們發現應用“奇偶特性”確實可以幫助我們更快地解決某種類型的題目。當然，“奇偶特性”也不是一成不變的，各位考生應該靈活應用，想要了解更多的“奇偶特性”的妙趣，各位考生可繼續關注華圖教育。

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：