<u id="udx2b"></u>
2021-07-11 15:21:56 公務員考試網 
 文章來源:遼寧分院
文章來源:遼寧分院
伴隨著公務員崗位的熱度不斷增加,越來越多的小伙伴投身到公務員考試的大軍當中,作為一名華圖資深的數量關系與資料分析科目的老師,為了更好地授課,也采訪過很多同學關于考試內容的認知,很多人的反饋都是關于數量關系的吐槽,認為這部分內容太難、很難得分、沒時間做等,最后也就放棄關于數量的學習了,但這是非常不明智的,因為在數量關系的內容當中,只要掌握好方法,就可以快速而準確地解決一些題目。今天給大家講解的賦零法,就是能夠幫助大家快速解決相關題型,翻身做主人的方法。
【例1】木匠加工2張桌子和4張凳子共需要10個小時,加工4張桌子和8張椅子需要22個小時。問如果加工桌子、凳子和椅子各10張,共需要多少小時?
A. 47.5 B. 50
C. 52.5 D. 55
觀察這道題,我們可以發現這是關于三個變量的方程題,設加工1張桌子、凳子和椅子分別需要x、y、z小時,根據題意,可列式為![]() ,這是關于三個未知數且只有兩個式子的不等方程組,通過正常的解方程組是很難求出每一個未知數的,而且問題求的還是
,這是關于三個未知數且只有兩個式子的不等方程組,通過正常的解方程組是很難求出每一個未知數的,而且問題求的還是![]() ,那么這道題應該如何計算呢?觀察問題,可以通過配系數法把所列出的方程進行搭配,只要能夠配出關于x、y、z系數相同的式子,即可求出答案,通過
,那么這道題應該如何計算呢?觀察問題,可以通過配系數法把所列出的方程進行搭配,只要能夠配出關于x、y、z系數相同的式子,即可求出答案,通過![]() ,可以得到
,可以得到![]() ,所以
,所以![]() 。
。
配系數法是非常適合解決這類不定方程組問題的,但是所存在的問題也很大,比如數據并不像題中所給的那么有規律,或者如何能夠快速而準確地配出問題中所需要的系數等,在時間非常緊張的考試當中,這種問題就更為突出了。
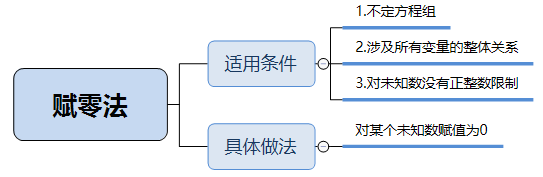
那么對于這類題有沒有更加好用的方法呢?答案是肯定的,就是我們要講解的賦零法。使用此方法的題目特征是:不定方程組且所求問題涉及所有變量的整體關系,其方法就是賦所列不定方程組中的任一未知數為0,進而求得其他未知數。對于這道題來說,可以賦x為0,則![]() ,最終得到
,最終得到![]() 。有沒有感覺到飛一樣的計算速度呢?這就是我們考試中必須要掌握的方法之一!
。有沒有感覺到飛一樣的計算速度呢?這就是我們考試中必須要掌握的方法之一!
賦零法之所以可以使用的原因就在于如果不定方程組中對于未知數沒有正整數的限制,且問題求的是關于所有變量的整體而非某一個未知數時,其實未知數解的組合是有無窮多個的,在某個組合中必然存在某一個未知數為0的情況,既然存在,那么我們就可以反過來令某一個未知數為0,求其他未知數的解,最后問題求的是涉及所有未知數的整體,這個整體是固定不變的,不會受單個未知數影響。
剛才我們也提到賦零法應用的前提中有一個“對未知數沒有正整數限制”,那如果有限制,將怎么樣呢?我們看一道題。
【例2】在超市購物,如果買2件甲商品、3件乙商品,共花費109元;如果買6件乙商品、1件丙商品,共花費104元,三種商品售價均為質數。若甲、乙、丙三種商品各買1件,需要多少元錢?
A. 37 B. 48
C. 57 D. 59
根據題意,設甲、乙、丙三種商品售價分別為x、y、z元,可列式為![]() ,
,![]() ,由于問題求的是
,由于問題求的是![]() 這個整體,采用賦零法,賦y為0,得到
這個整體,采用賦零法,賦y為0,得到![]() ,
,![]() ,則
,則![]() ,很明顯沒有答案,賦零法在這道題中不適用的原因是題中“三種商品售價均為質數”,即限定了這三個未知數均是正整數。正確的做法是6y和104均為偶數,所以z為偶數,z又是質數,得到z為2,代入式子②中,得到y為17,再代入到式子①中,得到x為29,則
,很明顯沒有答案,賦零法在這道題中不適用的原因是題中“三種商品售價均為質數”,即限定了這三個未知數均是正整數。正確的做法是6y和104均為偶數,所以z為偶數,z又是質數,得到z為2,代入式子②中,得到y為17,再代入到式子①中,得到x為29,則![]() 。因此,選擇B選項。
。因此,選擇B選項。
綜上所述,我們知道賦零法的應用是非常簡單的,能夠幫助我們在對應題目中快速得到答案,但是也要注意這種方法使用的范圍:非限定性不定方程(對未知數沒有正整數的限定),且要求問題所求的是涉及所有變量的整體關系,具體參考下圖。


| ↓↓↓↓2024年國家公務員考試相關推薦↓↓↓↓ | |||
| 公考第一課 | 2024版國考圖書 | 第18版5100題 | 申論答題紙 |
| 系統提升班plus | 筆試悅享班 | 歷年臻題 | APP會員年卡 |
相關內容推薦:
2024年國家公務員考試數量關系
2024年國家公務員考試資料分析

貼心微信客服

貼心微博客服
上一篇:數量關系備考類:賦值法應用

報名條件?
崗位選擇?
筆試科目?
面試方式?
......

 在線客服×
在線客服×國家公務員考試公告 國家公務員考試大綱 國家公務員考試專業分類目錄 國家公務員考試職位表 國家公務員考試報名入口 國家公務員考試報考條件 國家公務員考試報名費用 國家公務員考試報名人數 國家公務員考試報名確認 國家公務員考試準考證打印 國家公務員考試行測備考 國家公務員考試申論備考 國家公務員考試考試時間 國家公務員考試考試流程 國家公務員考試考試科目 國家公務員考試答題須知 國家公務員考試考場規則 國家公務員考試真題解析 國家公務員考試成績查詢 國家公務員考試分數線 國家公務員面試公告 國家公務員面試名單 國家公務員考試資格復審 國家公務員考試調劑名單 國家公務員面試技巧 國家公務員面試禮儀 國家公務員結構化面試 國家公務員無領導小組討論 國家公務員考試體檢考察 國家公務員考試錄用公示