2022省考行測備考之如何解答行程模塊中的相遇問題

行程問題在公務員的行測考試中不僅是一個高頻考點，也是一個難點問題，因為它的變化形式多種多樣，且存在多類陷阱，非常容易出錯。

對于行程問題，其中一個核心的公式就是：“路程=速度×時間”，萬變不離其宗，不管多復雜的題，最后都是用這個公式進行求解的，而這里的難點就在于速度和路程以及運動方式的不斷變化，導致我們不能快速準確地找到其中這些量。其中比較難的一個模型就是相遇追及的問題，今天我們就重點來談一下行程模塊中的相遇問題。

什么是相遇問題呢?兩個運動的物體同時由兩地出發相向而行，在途中相遇。這類應用題叫做相遇問題。這里面要注意的就是這兩個物體是同時出發，也就意味著相遇時他們運動的時間是一樣的。

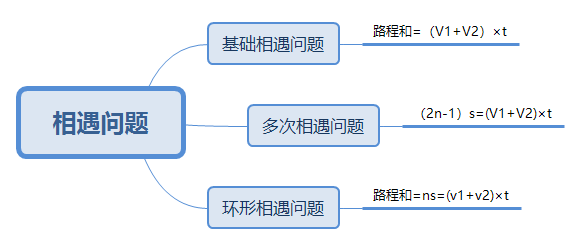
一、基礎相遇問題

對于基礎的相遇問題中有這樣的公式存在：

“總路程S=V1t+V2t”

在題目中出現相關條件，比如兩人同時相向而行時，就可以考慮利用這個公式，如例1這道題：

【例1】兩個人帶著寵物狗玩游戲，兩人相距200米，并以相同速度1米/秒相向而行，與此同時，寵物狗以3米/秒的速度，在兩人之間折返跑，當兩人相距60米時，那么寵物狗總共跑的距離為()。

A.270米B.240米

C.210米D.300米

【解析】兩人從相距200米運動到相距60米時，兩人的相對運動距離為200-60=140，由相遇問題公式可知140=(1+1)×t，解得t=70秒，因此寵物狗跑的路程為70×3=210米，所以本題答案選擇C。

二、直線型兩端出發多次相遇問題

相遇問題還有一類比較難的叫做多次相遇，即在同一個時間段內兩人多次往返運動，產生了多次相遇。多次相遇問題中存在這樣的公式：

“（2n-1）S=V1t+V2t”

多次相遇的問題乍一看是比較難的，但是利用公式來解答，就會變得很簡單。如例2這道題：

【例2】在一次航海模型展示活動中，甲乙兩款模型在長100米的水池兩邊同時開始相向勻速航行，甲款模型航行100米要72秒，乙款模型航行100米要60秒，若調頭轉身時間略去不計，在12分鐘內甲乙兩款模型相遇次數是：()。

A.9B.10

C.11D.12

【解析】往返多次相遇問題。行程問題。由題意，12分鐘時，甲、乙模型行駛的路程分別為1000米和1200米，兩車的路程和為2200米，根據公式：路程和=(2n-1)×S，解得n=11.5。故兩模型相遇了11次。因此，本題答案為C選項。

三、環形相遇問題

相遇問題中另一類的叫做環形相遇，環形相遇中存在的公式有以下三個：

環形周長=(大速度+小速度)×異向運動的兩人相遇時間

環線型n次相遇，共同行走的距離=n×環線長度。

例如例3這道題：

【例3】環形跑道長400米，老張、小王、小劉從同一地點出發，圍繞跑道分別慢走、跑步和騎自行車。已知三人速度分別為1米/秒，3米/秒和6米/秒。問小王第3次超越老張時，小劉已超越小王多少次?()

A.3次B.4次

C.5次D.6次

【解析】小王和老張的速度差為2米/秒，小劉和小王的速度差為3米/秒，因此相同時間內小劉和小王的路程差為小王和老張路程差的1.5倍，因此當小王與老張的路程差為3個全程時，小劉與老王的路程差為3×1.5=4.5個全程，因此，小劉超越小王4次。選擇B。

行程中的相遇問題，不同的題型解題公式不一樣，所以考生在做題之前一定要牢記相關公式，考試時識別出來題型后直接代入公式進行求解。

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：