行測備考知識點之兩端出發的直線相遇問題

在行測數量關系考試的試題中，行程問題出現的概率相對比較高。主要原因我想可能是，一方面從義務教育階段咱們就開始學習此類問題，另一方面，行程問題本身涵蓋的題型就比較多，涉及運動主體也會多一些，涉及題型分類大致如下圖：

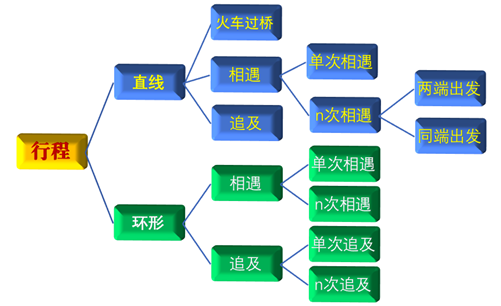
而相遇和追及問題是行程問題中永恒不變的話題，今天我們就來看看直線中兩端出發的多次相遇問題在解題時，有哪些技巧。

【例1】小車和客車從甲地開往乙地，貨車從乙地開往甲地，他們同時出發，貨車與小車相遇20分鐘后又遇客車。已知小車、貨車和客車的速度分別為75千米/小時、60千米/小時和50千米/小時，則甲、乙兩地的距離是：

A.205千米       B.203千米

C.201千米       D.198千米

【答案】D。華圖解析：很顯然，本道題屬于行程問題中兩端出發的直線相遇問題，因為在相遇后就不再涉及之后的過程了，所以屬于單次相遇。按照相遇問題的基本公式S=(V1+V2)×T，假如我們設甲乙兩地距離為S，貨車和小車相遇的時間為T1，可以根據題意，列出貨車與小車相遇的方程：S=(60+75)×T1，貨車與客車相遇的方程為：S=，則兩個方程聯立解得S=198。故選擇D選項。本題屬于簡單的單次相遇，直接按照常見的直線相遇問題的公式列方程即可解決，那么如果遇到下面這種多次相遇呢?

【例2】甲、乙兩名運動員在長100米的跑道上練習短跑，甲的速度為8.5m/s，乙的速度為7.5m/s。兩人同時分別從跑道的兩端相向運動做折返跑，不計運動員轉向及加速的時間。起跑后的1分鐘內，兩人共相遇了( )次。

A. 3     B. 4

C. 5     D. 6

【答案】C。華圖解析：本道題涉及到的問題就比較復雜了，可以看到甲乙兩人的速度和是每秒鐘8.5+7.5=16m/s，100米的距離，肯定用不了1分鐘兩人就會第一次相遇。接下來，我們有的同學可能會這么來解題：16×60÷100=9.6次≈9次(9.6次表示還不到10次，故是9次)，但是你會發現答案中卻沒有9次，問題出現在哪里呢?讓我們先來看看下面甲乙兩人在長度為S的兩端同時出發的相遇過程圖：

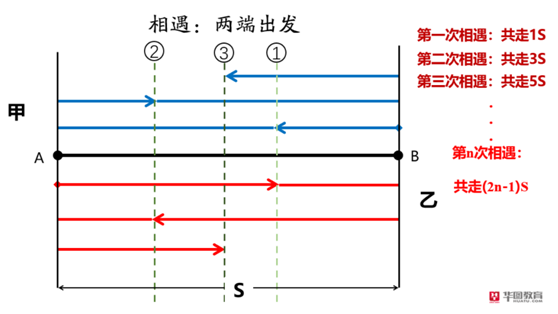
通過這張相遇過程圖，我們知道，兩者第一次相遇，甲乙一共走過的路程是S，而第二次相遇，甲乙一共走過的過程是3S，第三次相遇，甲乙共走過5S的總路程……由此我們總結出來，若甲乙兩人第n次相遇，則他們倆走過的總路程應該為(2n-1)S，根據最原始的單次相遇公式，可以得出，在甲乙兩者n次相遇時，他倆走過的總路程(2n-1)S和甲乙的速度V1、V2三者的關系是：(2n-1)S=(V1+V2)×T，此處的T是甲乙兩人相遇n次所花時間。由此，我們知道，例2中兩者運動過程是滿足這個公式的，我們把題目中已知條件代入公式，得到：(2n-1)×100=(7.5+8.5)×60，得到n=5.3≈5次(5.3次表示還不到6次，故是5次)，故本題選擇C選項。

通過上面的習題解答和過程的總結，我們得出(2n-1)S=(V1+V2)×T這樣一個直線行程兩端出發n次相遇中的兩人速度和兩地距離、及在一定時間內相遇次數關系的公式。今后再遇到此類題目，我們就可以運用這個公式去解題了，所以說，同學們在學習數量關系的過程中，要學會不斷總結，找出同一類問題中共同的本質，這樣才能提高學習效率，進而不斷進步!

【省考面試禮包】|【省考面試系統提升】|【省考面試圖書】|【面試題庫】

相關內容推薦：