<u id="udx2b"></u>
2021-08-26 10:43:19 公務員考試網 
 文章來源:山東分院
文章來源:山東分院
相遇問題是數量關系中一類較為常考的題型,同樣也是技巧性較強的題型。雖然相遇問題看似類型較為復雜,分成多種情況,但實際上本質就是找到問題的核心所在。考查考生的邏輯思維能力,通過使用特殊的技巧解決相遇問題。下面就相遇問題的題型進行具體分析:
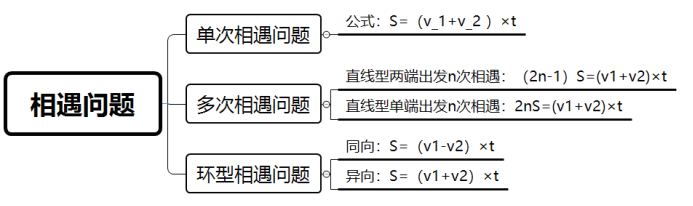
一、單次相遇問題
在相遇問題中,凡是方向相反的都可以看成相遇問題。引用公式![]() 。
。
【例1】甲、乙兩人沿直線從A地步行至B地,丙從B地步行至A地。已知甲、乙、丙三人同時出發,甲和丙相遇后5分鐘,乙與丙相遇。如果甲、乙、丙三人的速度分別為85米/分鐘、75米/分鐘、65米/分鐘。問AB兩地的距離為多少米?
A. 8000米
B. 8500米
C. 10000米
D. 10500米
【解析】第一步,本題考查行程問題,屬于相遇追及類,用方程法解題。
第二步,設AB兩地的距離為S,甲丙相遇時間為t,由甲丙相遇可得:S=(85+65)×t①;由甲丙相遇5分鐘后乙丙相遇可得:S=(75+65)×(t+5)②。聯立①②,解得S=10500米。
因此,選擇D選項。
在這道題中,核心在于無論甲乙相遇還是乙丙相遇,走的路程總和都為AB兩地之間的距離,這就是典型的相遇問題中直線型單次相遇,直接代入公式即可。
二、多次相遇問題
在多次相遇問題中,要先識別是屬于兩端出發還是單端出發問題,再代入公式,直線型兩端出發n次相遇:(2n-1)S=(![]() )×t;以及直線型單端出發n次相遇:2nS=(
)×t;以及直線型單端出發n次相遇:2nS=(![]() )×t。
)×t。
【例二】在一次航海模型展示活動中,甲乙兩款模型在長100米的水池兩邊同時開始相向勻速航行,甲款模型航行100米要72秒,乙款模型航行100米要60秒,若調頭轉身時間略去不計,在12分鐘內甲乙兩款模型相遇次數是:
A. 9
B. 10
C. 11
D. 12
【解析】第一步,本題考查行程問題,屬于相遇追及類。
第二步,12分鐘=720秒。設共相遇n次,則總共行駛距離S=(2n-1)S,利用兩端出發多次相遇問題公式(2n-1)S=(![]() )×t,可得(2n-1)×100=(
)×t,可得(2n-1)×100=(![]() )×720。
)×720。
第三步,解得n=11.5,故迎面相遇11次。
因此,選擇C選項。
在這道題中,問題的核心在于看出這是單端還是兩端出發,甲乙兩款模型從兩邊開始航行,證明是兩端出發問題,因此,引用公式(2n-1)S=(![]() )×t。
)×t。
三、環型相遇問題
在環型問題中,在同一起點出發,要先識別方向是同向還是異向相遇,同向出發證明速度快的比速度慢的多跑了一圈,再代入公式即可,同向:S=(![]() )×t;以及異向:S=(
)×t;以及異向:S=(![]() )×t。
)×t。
【例三】甲、乙兩人在一條400米的環形跑道上從相距200米的位置出發,同向勻速跑步。當甲第三次追上乙的時候,乙跑了2000米。問甲的速度是乙的多少倍?
A. 1.2
B. 1.5
C. 1.6
D. 2.0
【解析】第一步,本題考查行程問題,屬于相遇追及類。
第二步,環形同點同向出發每追上一次,甲比乙多跑一圈。第一次由于是不同起點,甲比乙多跑原來的差距200米;之后兩次追上都多跑400米,甲一共比乙多跑200+400×2=1000(米)。乙跑了2000米,甲跑了3000米,時間相同,則速度比與路程比也相同,可知甲的速度是乙的3000÷2000=1.5倍。
因此,選擇B選項。
在這道題中,因為同向出發,所以代入公式S=(![]() )×t,又因為起點不同,起點相距200米,因此第一次甲比乙多走200米,就能夠通過乙的路程算出甲所走的全程。
)×t,又因為起點不同,起點相距200米,因此第一次甲比乙多走200米,就能夠通過乙的路程算出甲所走的全程。

| ↓↓↓↓2024年國家公務員考試相關推薦↓↓↓↓ | |||
| 公考第一課 | 2024版國考圖書 | 第18版5100題 | 申論答題紙 |
| 系統提升班plus | 筆試悅享班 | 歷年臻題 | APP會員年卡 |
相關內容推薦:
2024年國家公務員考試數量關系

貼心微信客服

貼心微博客服
下一篇:2022國考行測備考之基礎概率

報名條件?
崗位選擇?
筆試科目?
面試方式?
......

 在線客服×
在線客服×國家公務員考試公告 國家公務員考試大綱 國家公務員考試專業分類目錄 國家公務員考試職位表 國家公務員考試報名入口 國家公務員考試報考條件 國家公務員考試報名費用 國家公務員考試報名人數 國家公務員考試報名確認 國家公務員考試準考證打印 國家公務員考試行測備考 國家公務員考試申論備考 國家公務員考試考試時間 國家公務員考試考試流程 國家公務員考試考試科目 國家公務員考試答題須知 國家公務員考試考場規則 國家公務員考試真題解析 國家公務員考試成績查詢 國家公務員考試分數線 國家公務員面試公告 國家公務員面試名單 國家公務員考試資格復審 國家公務員考試調劑名單 國家公務員面試技巧 國家公務員面試禮儀 國家公務員結構化面試 國家公務員無領導小組討論 國家公務員考試體檢考察 國家公務員考試錄用公示