2022省考行測(cè)備考:方程法之巧設(shè)未知數(shù)

在公考中，數(shù)量關(guān)系的各大類(lèi)題型幾乎都離不開(kāi)方程法這一解題方法，方程法也是考生們?cè)谝酝鶎W(xué)習(xí)經(jīng)歷中用的比較多的方法，相信各位考生對(duì)這一解題方法并不陌生，但是在以往的學(xué)習(xí)過(guò)程中，我們經(jīng)常設(shè)未知數(shù)的方法就是看問(wèn)題所問(wèn)去設(shè)未知數(shù)，這就導(dǎo)致很多考生在解方程的過(guò)程中耽誤了大量的時(shí)間，今天，安徽華圖帶著大家來(lái)看看如何在方程法中巧設(shè)未知數(shù)以加快解題速度。

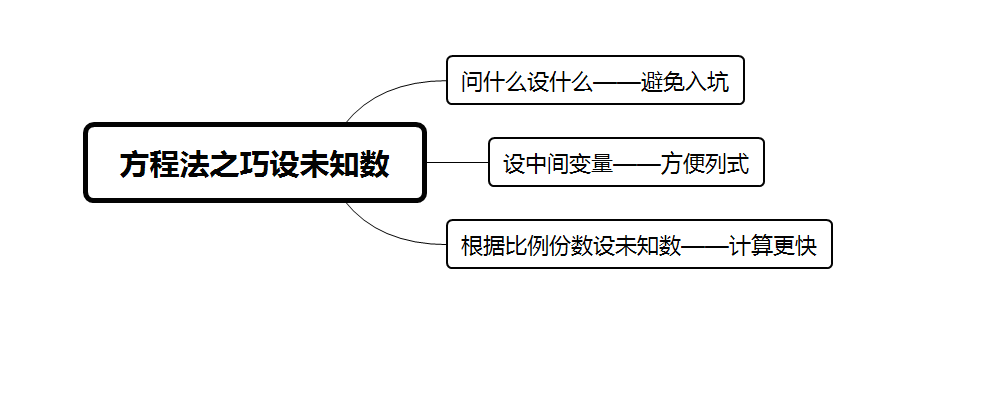
一、巧設(shè)未知數(shù)之問(wèn)什么設(shè)什么——避免入坑

對(duì)于有的題目，無(wú)論你設(shè)誰(shuí)為x都不會(huì)影響你的列式或者計(jì)算，這種情況下就問(wèn)什么設(shè)什么，避免掉入出題人設(shè)計(jì)的陷阱中，比如下面這個(gè)例題。

【例】甲、乙兩人從湖邊某處同時(shí)出發(fā)，沿兩條環(huán)湖路各自勻速行走。甲恰好用2小時(shí)回到出發(fā)點(diǎn)，比乙晚到20分鐘，多走了2800米。若甲每分鐘比乙多走10米，則甲行走的速度是：

A.4.2千米/小時(shí)

B.4.5千米/小時(shí)

C.4.8千米/小時(shí)

D.5.4千米/小時(shí)

【答案】D

【解析】設(shè)甲的速度為x米/分鐘，那么乙的速度為x-10米/分鐘。由題意甲走的時(shí)間為120分鐘，距離為120x;乙走的時(shí)間為120-20=100分鐘，距離為100(x-10)。根據(jù)多走了2800米可列方程120x-100(x-10)=2800，解得x=90，那么甲的速度為90米/分鐘=5400米/小時(shí)，即5.4千米/小時(shí)。

因此，選擇D選項(xiàng)。

本題設(shè)甲或乙為x并不會(huì)對(duì)列式或者計(jì)算造成影響，故可直接設(shè)問(wèn)題所問(wèn)，避免掉入出題人設(shè)計(jì)的乙的速度陷阱中。

二、巧設(shè)未知數(shù)之設(shè)中間變量——方便列式

【例】某單位舉行“青藍(lán)工程”師徒結(jié)隊(duì)活動(dòng)。工齡在16年以上的作為高級(jí)導(dǎo)師，每人必須帶2個(gè)或者3個(gè)徒弟。工齡在11至15年的有12人作為初級(jí)導(dǎo)師，每人必須帶1個(gè)徒弟。工齡在5年以下的有28人作為徒弟。如果帶3個(gè)徒弟的高級(jí)導(dǎo)師人數(shù)比帶2個(gè)徒弟的高級(jí)導(dǎo)師人數(shù)多兩人，那么該單位參與這項(xiàng)活動(dòng)的一共有：

A.43人

B.46人

C.49人

D.52人

【答案】B

【解析】設(shè)帶2個(gè)徒弟的高級(jí)導(dǎo)師有x人，那么帶3個(gè)徒弟的高級(jí)導(dǎo)師有(x+2)人。可列方程：2x+3(x+2)+12=28，解得x=2，那么帶3個(gè)徒弟的高級(jí)導(dǎo)師有4人，一共有2+4+12+28=46(人)。

因此，選擇B選項(xiàng)。

在本題中如果設(shè)總?cè)藬?shù)，那就不好求了，找到本題關(guān)鍵就是缺高級(jí)導(dǎo)師數(shù)量，故設(shè)未知數(shù)時(shí)設(shè)高級(jí)導(dǎo)師數(shù)量，就能方便列式解決了。

三、巧設(shè)未知數(shù)之設(shè)比例份數(shù)——計(jì)算更快

當(dāng)題目出現(xiàn)比例份數(shù)時(shí)，根據(jù)比例份數(shù)去設(shè)未知數(shù)，能夠讓所列方程盡可能不出現(xiàn)分?jǐn)?shù)或者小數(shù)，能夠更快計(jì)算出結(jié)果。比如下面這個(gè)例題。

【例】某農(nóng)場(chǎng)有A、B、C三個(gè)糧倉(cāng)，原先糧食儲(chǔ)量之比為5:9:10，今年豐收后每個(gè)糧倉(cāng)新增加的糧食儲(chǔ)量相同，A、B兩個(gè)糧倉(cāng)的儲(chǔ)量之比變?yōu)?:5，則今年豐收后三個(gè)糧倉(cāng)的儲(chǔ)存總量比原先增加：

A.12.5%

B.15%

C.17.5%

D.20%

【答案】A

【解析】第二步，由A、B、C儲(chǔ)量比例為5∶9∶10，設(shè)A、B、C儲(chǔ)量分別為5x、9x、10x，共24x。設(shè)各倉(cāng)新增y，根據(jù)A、B儲(chǔ)量比變?yōu)?∶5，可列方程(5x+y)∶(9x+y)=3∶5，解得x=y。則豐收后三倉(cāng)儲(chǔ)量新增3y，即3x，增加3x÷24x=12.5%。

因此，選擇A選項(xiàng)。

本題便是出現(xiàn)比例份數(shù)的題目，如果不根據(jù)比例份數(shù)設(shè)未知數(shù)，必然加重解題的負(fù)擔(dān)。

四、小結(jié)

在數(shù)量關(guān)系中遇到方程法的題目，設(shè)未知數(shù)時(shí)一定要根據(jù)不同的情形去設(shè)置未知數(shù)，另外在解出x的值之后一定要回頭看看問(wèn)題所問(wèn)，避免掉入出題人設(shè)置的陷阱中。在這里，華圖教育祝大家一舉成公!

【省考面試禮包】|【省考面試系統(tǒng)提升】|【省考面試圖書(shū)】|【面試題庫(kù)】

相關(guān)內(nèi)容推薦：